📋 Table of Contents
- 1. Introduction to Loan Calculations
- 2. Understanding Loan Basics
- 3. Simple Interest Calculations
- 4. Compound Interest Mastery
- 5. Monthly Payment Formulas
- 6. Amortization Schedules
- 7. Different Loan Types
- 8. Advanced Calculation Techniques
- 9. Real-World Examples
- 10. Professional Tools and Resources
- 11. Optimization Strategies
- 12. Conclusion
1. Introduction to Loan Calculations
Understanding how to calculate loan payments and interest is one of the most valuable financial skills you can develop. Whether you're considering a mortgage, auto loan, personal loan, or business financing, the ability to accurately calculate payments, interest costs, and total loan expenses empowers you to make informed decisions that can save thousands of dollars over the life of your loans.
In today's complex financial landscape, lenders offer various loan products with different interest rates, terms, and payment structures. Without a solid understanding of loan mathematics, borrowers often find themselves accepting unfavorable terms or failing to recognize better opportunities. This comprehensive guide will transform you from a passive borrower into an informed financial decision-maker.

The mathematics behind loan calculations might seem intimidating at first, but once you understand the fundamental principles and formulas, you'll find that most loan calculations follow predictable patterns. We'll start with basic concepts and gradually build up to more complex scenarios, ensuring you develop both theoretical knowledge and practical skills.
Throughout this guide, we'll use real-world examples and provide access to professional-grade calculators that will help you verify your calculations and explore different scenarios. By the end of this comprehensive tutorial, you'll be able to calculate loan payments manually, understand how interest affects your total costs, and optimize your borrowing strategy like a financial professional.
2. Understanding Loan Basics
2.1 Essential Loan Components
Before diving into calculations, it's crucial to understand the fundamental components that make up any loan. These elements form the foundation of all loan calculations and directly impact your monthly payments and total interest costs.
Principal Amount
The principal is the original amount of money you borrow from a lender. This is the base amount on which interest is calculated. For example, if you're buying a $300,000 house and making a $60,000 down payment, your loan principal would be $240,000. Understanding the principal is essential because it directly affects both your monthly payments and the total interest you'll pay over the loan's lifetime.
Interest Rate
The interest rate represents the cost of borrowing money, expressed as a percentage of the principal. Interest rates can be fixed (remaining constant throughout the loan term) or variable (changing based on market conditions). The interest rate significantly impacts your monthly payments and total loan cost. Even a small difference in interest rates can result in thousands of dollars in savings or additional costs over the life of a loan.

Loan Term
The loan term is the length of time you have to repay the loan, typically expressed in months or years. Common loan terms include 15, 20, or 30 years for mortgages, and 3-7 years for auto loans. Longer terms generally result in lower monthly payments but higher total interest costs, while shorter terms mean higher monthly payments but less interest paid overall.
Payment Frequency
Most loans require monthly payments, but some allow bi-weekly, weekly, or other payment schedules. The payment frequency affects how interest accrues and can significantly impact the total interest paid over the loan's life. Bi-weekly payments, for example, can reduce the loan term and total interest substantially.
2.2 Types of Interest
Understanding different types of interest is crucial for accurate loan calculations. The type of interest used affects how your payments are applied and how much you'll ultimately pay.
Simple Interest
Simple interest is calculated only on the principal amount. While less common in modern lending, understanding simple interest provides a foundation for more complex calculations. The formula is straightforward: Interest = Principal × Rate × Time.
Compound Interest
Compound interest is calculated on both the principal and previously accumulated interest. This is the most common type of interest used in loans and investments. Compound interest can work for you (in savings accounts) or against you (in loans), making it essential to understand its mechanics.
💡 Pro Tip
Always ask lenders whether they use simple or compound interest, and how frequently interest compounds. This information is crucial for accurate payment calculations and comparing loan offers.
2.3 Amortization vs. Interest-Only Loans
Most traditional loans are amortizing loans, where each payment includes both principal and interest. Early payments consist mostly of interest, while later payments apply more toward the principal. Interest-only loans, where you pay only interest for a specified period, require different calculation methods and carry different risks.
Understanding these fundamental concepts is essential before moving to specific calculation formulas. Each component interacts with others to determine your monthly payment amount and total loan cost. Use our Professional Loan Calculator to explore how changes in these variables affect your loan terms.
3. Simple Interest Calculations
Simple interest calculations form the foundation of loan mathematics. While most modern loans use compound interest, understanding simple interest is essential for grasping more complex concepts and for certain types of short-term loans and financial instruments.
3.1 The Simple Interest Formula
Simple Interest Formula
Where:
- I = Interest amount
- P = Principal (initial loan amount)
- R = Annual interest rate (as a decimal)
- T = Time period (in years)
3.2 Step-by-Step Calculation Process
- Convert the interest rate to decimal form: Divide the percentage rate by 100. For example, 5% becomes 0.05.
- Convert the time period to years: If you have months, divide by 12. For days, divide by 365.
- Apply the formula: Multiply Principal × Rate × Time to get the interest amount.
- Calculate total amount: Add the interest to the principal to get the total amount owed.
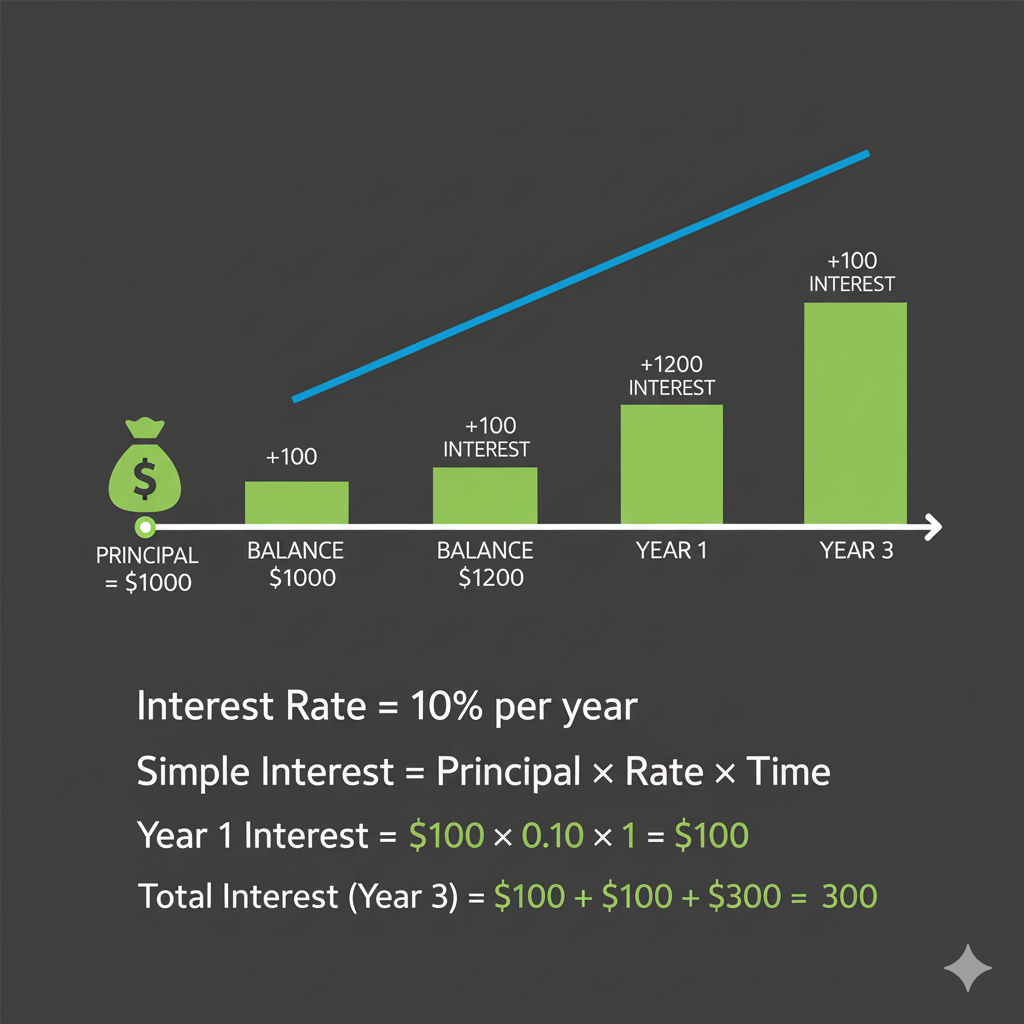
📊 Simple Interest Example
Scenario: You borrow $10,000 at 6% annual simple interest for 3 years.
Calculation:
- P = $10,000
- R = 6% = 0.06
- T = 3 years
- I = $10,000 × 0.06 × 3 = $1,800
- Total Amount = $10,000 + $1,800 = $11,800
3.3 Monthly Payment Calculation for Simple Interest Loans
For simple interest loans with equal monthly payments, you can calculate the monthly payment by dividing the total amount (principal plus interest) by the number of payment periods.
Monthly Payment Formula (Simple Interest)
Or alternatively:
📊 Monthly Payment Example
Using the previous example ($10,000 at 6% for 3 years):
- Total Amount = $11,800
- Number of Months = 3 × 12 = 36 months
- Monthly Payment = $11,800 ÷ 36 = $327.78
3.4 Applications of Simple Interest
Simple interest is commonly used in:
- Short-term personal loans: Some payday loans and short-term personal loans use simple interest calculations.
- Auto loans: Many auto loans use simple interest, though they're calculated daily.
- Some business loans: Certain commercial lending products use simple interest structures.
- Savings accounts: Basic savings accounts often use simple interest calculations.
💡 Important Note
While the concept is called "simple interest," many loans that claim to use simple interest actually calculate interest daily and compound it, which can result in slightly higher costs than true simple interest calculations.
Understanding simple interest provides the foundation for more complex loan calculations. Practice these calculations with different scenarios to build your confidence before moving to compound interest formulas. Our Interest Rate Calculator can help you verify your simple interest calculations and explore different scenarios.
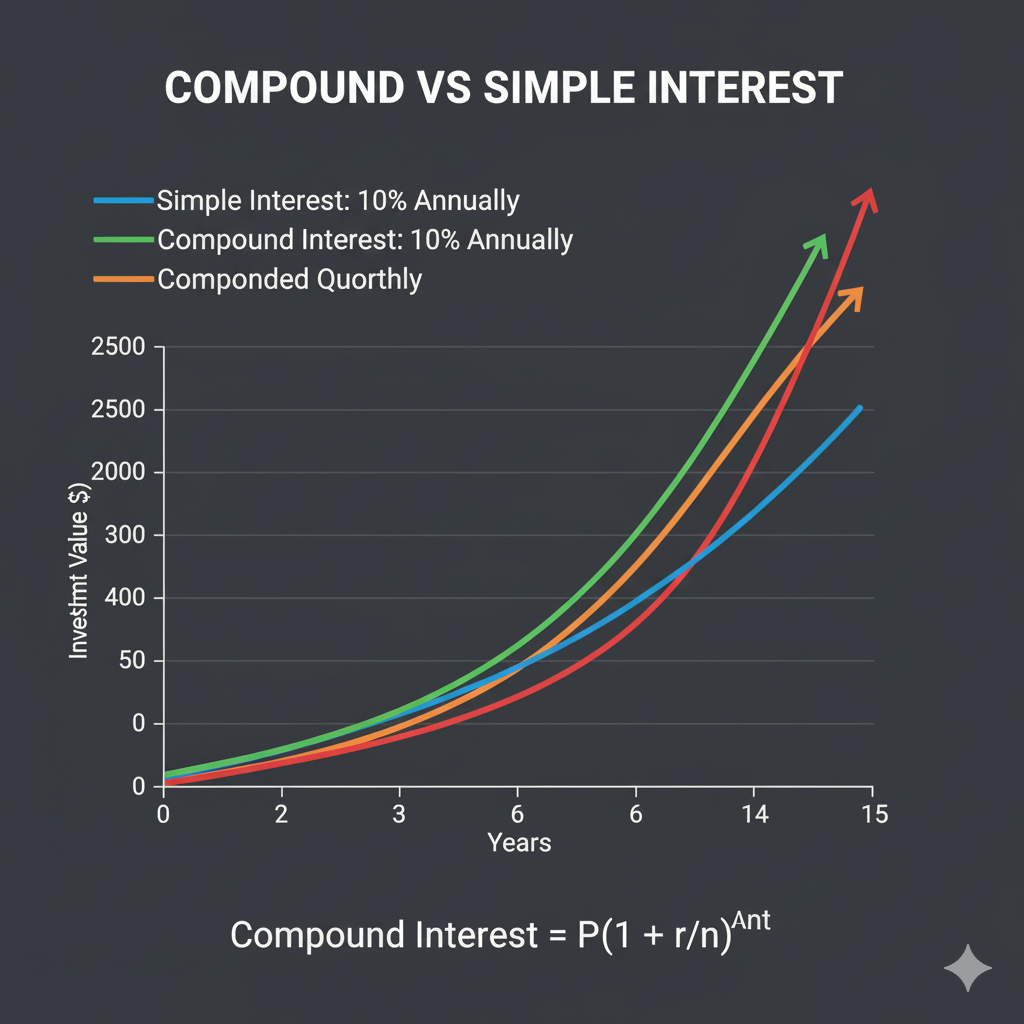
4. Compound Interest Mastery
Compound interest is the cornerstone of modern lending and investing. Unlike simple interest, compound interest calculates interest on both the original principal and previously earned interest. This compounding effect can work dramatically in your favor when investing, but it can significantly increase the cost of borrowing. Mastering compound interest calculations is essential for understanding most loan products available today.
4.1 The Compound Interest Formula
Compound Interest Formula
Where:
- A = Final amount (principal + interest)
- P = Principal (initial amount)
- r = Annual interest rate (as decimal)
- n = Number of times interest compounds per year
- t = Time in years
4.2 Understanding Compounding Frequency
The frequency of compounding significantly affects the total interest accumulated. Common compounding frequencies include:
| Compounding Frequency | Times per Year (n) | Impact on Interest |
|---|---|---|
| Annually | 1 | Lowest compound effect |
| Semi-annually | 2 | Moderate increase |
| Quarterly | 4 | Higher compound effect |
| Monthly | 12 | Common for loans |
| Daily | 365 | Maximum practical effect |
4.3 Detailed Calculation Examples
📊 Compound Interest Example - Monthly Compounding
Scenario: $50,000 loan at 7% annual interest, compounded monthly, for 5 years
Given:
- P = $50,000
- r = 7% = 0.07
- n = 12 (monthly compounding)
- t = 5 years
Calculation:
- A = $50,000(1 + 0.07/12)^(12×5)
- A = $50,000(1 + 0.005833)^60
- A = $50,000(1.005833)^60
- A = $50,000 × 1.4148
- A = $70,740
- Total Interest = $70,740 - $50,000 = $20,740
4.4 The Power of Compounding Frequency
Let's examine how different compounding frequencies affect the same loan:
📊 Compounding Frequency Comparison
Loan: $25,000 at 8% for 4 years
| Compounding | Final Amount | Total Interest |
|---|---|---|
| Annually (n=1) | $34,012 | $9,012 |
| Quarterly (n=4) | $34,273 | $9,273 |
| Monthly (n=12) | $34,349 | $9,349 |
| Daily (n=365) | $34,386 | $9,386 |
4.5 Continuous Compounding
For theoretical purposes and some financial instruments, interest may compound continuously. The formula for continuous compounding is:
Continuous Compounding Formula
Where e is Euler's number (approximately 2.71828)
4.6 Effective Annual Rate (EAR)
The Effective Annual Rate helps compare loans with different compounding frequencies by converting them to an equivalent annual rate.
Effective Annual Rate Formula
📊 EAR Calculation Example
Scenario: 6% annual rate compounded monthly
- EAR = (1 + 0.06/12)^12 - 1
- EAR = (1.005)^12 - 1
- EAR = 1.0617 - 1 = 0.0617
- EAR = 6.17%
💡 Borrower's Strategy
When comparing loan offers, always calculate the EAR to make accurate comparisons. A loan with a lower stated rate but more frequent compounding might actually cost more than a loan with a higher stated rate but less frequent compounding.
Understanding compound interest is crucial for making informed borrowing decisions. Use our Compound Interest Calculator to experiment with different scenarios and see how compounding affects your loan costs over time.
5. Monthly Payment Formulas
Calculating accurate monthly payments is perhaps the most practical skill in loan mathematics. Whether you're budgeting for a new home, car, or personal loan, knowing how to calculate monthly payments allows you to plan your finances effectively and negotiate better terms with lenders.
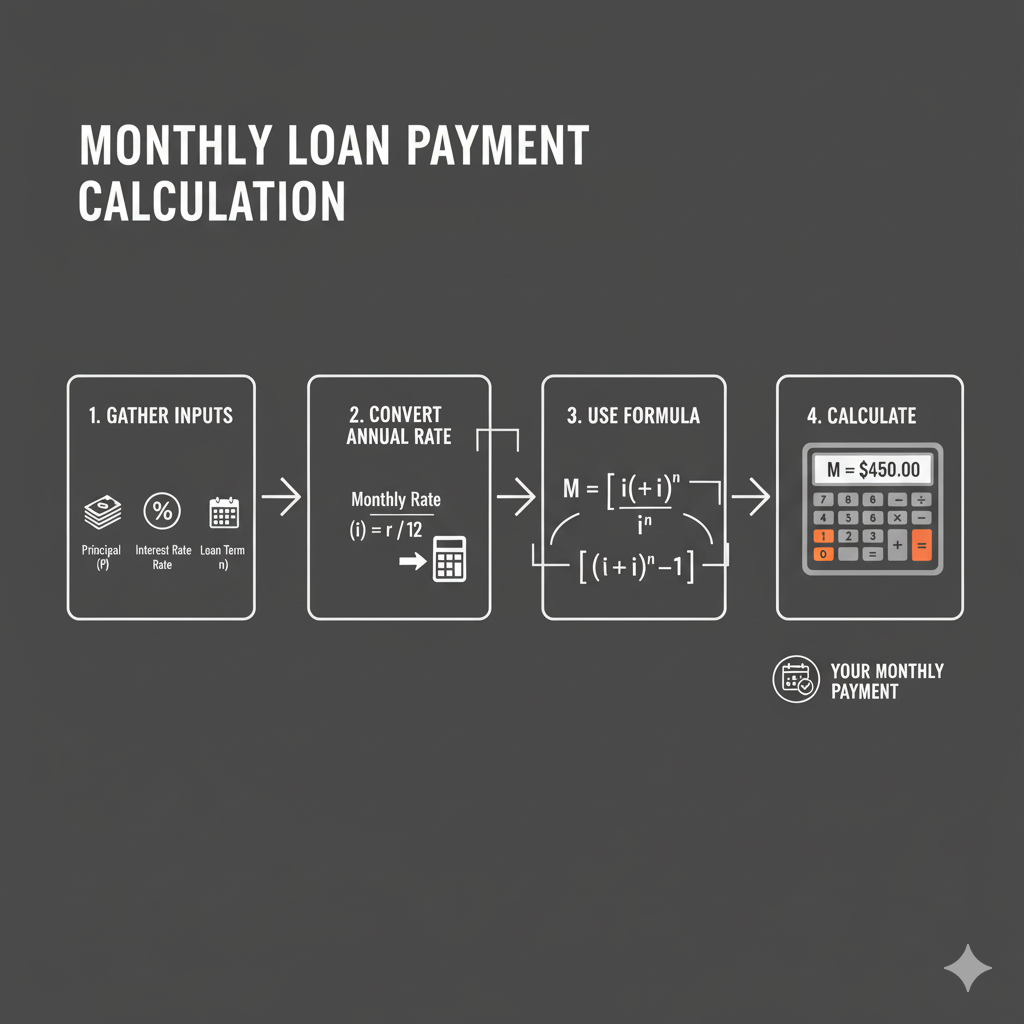
5.1 The Standard Monthly Payment Formula
The most commonly used formula for calculating monthly payments on amortizing loans is derived from the present value of an annuity formula. This formula accounts for compound interest and ensures that the loan is fully paid off by the end of the term.
Monthly Payment Formula (PMT)
Where:
- PMT = Monthly payment amount
- P = Principal loan amount
- r = Monthly interest rate (annual rate ÷ 12)
- n = Total number of payments (years × 12)
5.2 Step-by-Step Calculation Process
- Convert annual interest rate to monthly: Divide the annual rate by 12. For example, 6% annually becomes 0.06 ÷ 12 = 0.005 monthly.
- Calculate total number of payments: Multiply the loan term in years by 12. A 30-year loan has 30 × 12 = 360 payments.
- Calculate (1+r)^n: This is often the most complex part. Use a calculator with exponential functions.
- Apply the complete formula: Substitute all values and calculate the final monthly payment.
5.3 Comprehensive Calculation Example
📊 Monthly Payment Calculation Example
Scenario: $250,000 mortgage at 4.5% annual interest for 30 years
Step 1 - Identify variables:
- P = $250,000
- Annual rate = 4.5% = 0.045
- r = 0.045 ÷ 12 = 0.00375 (monthly rate)
- n = 30 × 12 = 360 payments
Step 2 - Calculate (1+r)^n:
- (1 + 0.00375)^360 = (1.00375)^360 = 3.8484
Step 3 - Apply the formula:
- PMT = $250,000 × [0.00375 × 3.8484] / [3.8484 - 1]
- PMT = $250,000 × [0.014432] / [2.8484]
- PMT = $250,000 × 0.005067
- PMT = $1,266.71
5.4 Alternative Payment Calculation Methods
5.4.1 Using Financial Calculator Functions
Most financial calculators and spreadsheet programs have built-in payment functions. In Excel, you can use the PMT function:
Excel PMT Function
Example: =PMT(0.045/12, 360, -250000) = $1,266.71
5.4.2 Approximation Methods
For quick estimates, you can use simplified approximation formulas, though these are less accurate:
Quick Approximation Formula
This provides a reasonable estimate for initial planning purposes.
5.5 Impact of Different Variables
Understanding how changes in loan variables affect monthly payments is crucial for loan optimization:
| Loan Amount | Interest Rate | Term (Years) | Monthly Payment |
|---|---|---|---|
| $200,000 | 4.0% | 30 | $954.83 |
| $200,000 | 5.0% | 30 | $1,073.64 |
| $200,000 | 4.0% | 15 | $1,479.38 |
| $300,000 | 4.0% | 30 | $1,432.25 |
5.6 Special Payment Scenarios
5.6.1 Interest-Only Payments
For interest-only loans, the monthly payment calculation is much simpler:
Interest-Only Payment Formula
5.6.2 Balloon Payments
Loans with balloon payments require modified calculations that account for the large final payment. The monthly payment formula becomes:
Balloon Payment Formula
Where B is the balloon payment amount
💡 Payment Optimization Tip
Small changes in interest rates have significant impacts on monthly payments and total interest costs. A 0.5% rate difference on a $300,000 30-year mortgage changes the monthly payment by about $87 and the total interest by over $31,000!
Mastering monthly payment calculations gives you the power to evaluate loan offers quickly and accurately. Practice these calculations with different scenarios, and use our Mortgage Calculator to verify your results and explore various loan scenarios.
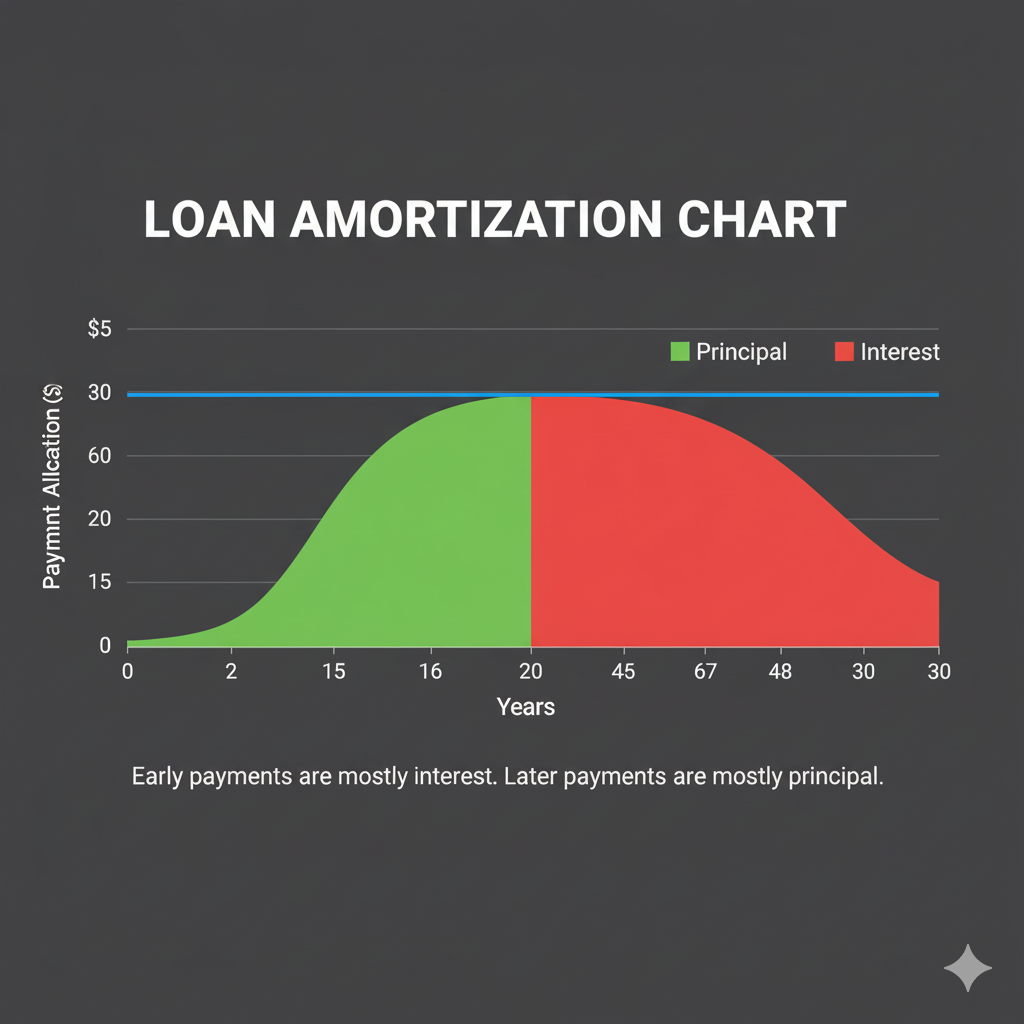
6. Amortization Schedules
An amortization schedule is a detailed table showing each payment over the life of a loan, breaking down how much of each payment goes toward principal and how much goes toward interest. Understanding amortization schedules is crucial for loan management, refinancing decisions, and tax planning. This knowledge allows you to see exactly how your loan balance decreases over time and how much interest you'll pay in any given period.
6.1 Understanding Amortization Mechanics
In an amortizing loan, each payment is the same amount, but the allocation between principal and interest changes over time. Early in the loan term, most of your payment goes toward interest, while later payments apply more toward the principal balance. This happens because interest is calculated on the remaining balance, which decreases with each payment.
6.2 Amortization Calculation Formulas
To create an amortization schedule, you need several key formulas:
Key Amortization Formulas
6.3 Step-by-Step Amortization Schedule Creation
- Calculate the monthly payment: Use the PMT formula from the previous section to determine the fixed monthly payment amount.
- Set up your schedule table: Create columns for Payment Number, Payment Amount, Interest Portion, Principal Portion, and Remaining Balance.
- Calculate each month's interest: Multiply the remaining balance by the monthly interest rate.
- Calculate the principal portion: Subtract the interest portion from the total monthly payment.
- Update the remaining balance: Subtract the principal portion from the previous balance.
- Repeat for each payment: Continue this process for every payment in the loan term.
6.4 Detailed Amortization Example
📊 Amortization Schedule Example
Loan Details: $100,000 at 5% annual interest for 10 years
Monthly Payment: $1,060.66 (calculated using PMT formula)
| Payment # | Payment | Interest | Principal | Balance |
|---|---|---|---|---|
| 1 | $1,060.66 | $416.67 | $643.99 | $99,356.01 |
| 2 | $1,060.66 | $414.00 | $646.66 | $98,709.35 |
| 3 | $1,060.66 | $411.29 | $649.37 | $98,059.98 |
| ... | ... | ... | ... | ... |
| 120 | $1,060.66 | $4.42 | $1,056.24 | $0.00 |
6.5 Key Amortization Insights
6.5.1 The 80/20 Rule in Early Payments
In the early years of most long-term loans, approximately 80% of your payment goes toward interest and only 20% toward principal. This ratio gradually reverses over the loan term. Understanding this helps explain why loan balances decrease slowly in the beginning.
6.5.2 Midpoint Analysis
At the midpoint of a 30-year mortgage, you've made half the payments but typically paid off only about 25-30% of the principal. This is due to the front-loaded interest structure of amortizing loans.
📊 30-Year Mortgage Midpoint Analysis
Loan: $300,000 at 4.5% for 30 years (Monthly payment: $1,520.06)
- After 15 years (180 payments):
- Total payments made: $273,611
- Interest paid: $185,432
- Principal paid: $88,179
- Remaining balance: $211,821
- Principal paid: Only 29.4% of original loan!
6.6 Advanced Amortization Concepts
6.6.1 Negative Amortization
Negative amortization occurs when monthly payments are less than the interest due, causing the loan balance to increase over time. This can happen with adjustable-rate mortgages or payment-option loans.
Negative Amortization Detection
6.6.2 Accelerated Amortization
Making extra principal payments accelerates amortization and can save substantial interest costs. Even small additional payments can significantly reduce the loan term and total interest.
📊 Extra Payment Impact
Original Loan: $200,000 at 4% for 30 years (Payment: $954.83)
With $100 extra monthly principal payment:
- New payoff time: 24.5 years (5.5 years earlier)
- Total interest saved: $37,816
- Total extra payments: $29,400
- Net savings: $8,416
6.7 Using Amortization Schedules for Decision Making
6.7.1 Refinancing Analysis
Amortization schedules help determine the optimal time to refinance. Compare the remaining balance and future interest payments on your current loan with the costs and payments of a new loan.
6.7.2 Prepayment Strategy
Use amortization schedules to identify the most effective times to make extra payments. Early in the loan term, extra payments have the greatest impact on total interest savings.
6.7.3 Tax Planning
For tax-deductible loans like mortgages, amortization schedules show exactly how much interest you'll pay each year, helping with tax planning and deduction calculations.
💡 Amortization Strategy
Review your amortization schedule annually to understand your loan's progress and identify opportunities for optimization. Consider making extra principal payments when you have surplus cash, especially early in the loan term.
Understanding amortization schedules empowers you to make informed decisions about loan management, prepayments, and refinancing. Use our Advanced Loan Calculator to generate detailed amortization schedules for your specific loans and explore different payment strategies.
7. Different Loan Types and Their Calculations
Different types of loans require different calculation approaches. Understanding the unique characteristics and calculation methods for various loan products is essential for making informed borrowing decisions. Each loan type has specific features that affect how interest is calculated, how payments are structured, and what the total cost will be over the loan's lifetime.
7.1 Fixed-Rate Loans
Fixed-rate loans maintain the same interest rate throughout the entire loan term, making them predictable and easy to calculate. The monthly payment remains constant, though the allocation between principal and interest changes over time through amortization.
7.1.1 Fixed-Rate Mortgage Calculations
Fixed-rate mortgages are the most common home loan type. They use the standard PMT formula we covered earlier, with some additional considerations for property taxes, insurance, and PMI (Private Mortgage Insurance).
Total Monthly Housing Payment
This is often called "PITI" (Principal, Interest, Taxes, Insurance)
📊 Fixed-Rate Mortgage Example
Loan: $350,000 at 4.25% for 30 years
- Principal & Interest: $1,721.14
- Property Taxes: $583.33 ($7,000 annually)
- Homeowner's Insurance: $125.00 ($1,500 annually)
- PMI: $145.83 (0.5% annually on loan amount)
- Total Monthly Payment: $2,575.30
7.2 Adjustable-Rate Mortgages (ARMs)
ARMs have interest rates that change periodically based on market conditions. These loans typically start with lower rates than fixed-rate mortgages but carry the risk of rate increases over time.
7.2.1 ARM Structure and Calculations
ARMs are typically described with two numbers (e.g., 5/1 ARM), where the first number is the initial fixed period and the second is how often the rate adjusts afterward.
ARM Rate Calculation
Subject to periodic and lifetime caps
📊 ARM Calculation Example
5/1 ARM: $300,000 loan, 3.5% initial rate, 2.5% margin, 2% periodic cap, 6% lifetime cap
Year 1-5: Fixed at 3.5% = $1,347.13 monthly
Year 6: If index is 2.8%, new rate = 2.8% + 2.5% = 5.3%
New payment: $1,659.18 (increase of $312.05)
7.3 Interest-Only Loans
Interest-only loans allow borrowers to pay only the interest for a specified period, typically 5-10 years. After this period, payments increase significantly to include principal repayment.
Interest-Only Payment Calculation
📊 Interest-Only Loan Example
Loan: $400,000 at 5% with 10-year interest-only period, then 20-year amortization
- Years 1-10: $1,666.67 monthly (interest only)
- Years 11-30: $2,639.82 monthly (principal + interest)
- Payment increase: $973.15 (58.4% jump!)
7.4 Auto Loans
Auto loans typically use simple interest calculated daily, though they function similarly to compound interest loans. Most auto loans are secured by the vehicle and have shorter terms than mortgages.
7.4.1 Auto Loan Calculation Specifics
Auto loans often include additional costs that affect the total financing amount:
Total Auto Loan Amount
📊 Auto Loan Calculation
Vehicle Purchase:
- Vehicle price: $35,000
- Sales tax (8%): $2,800
- Documentation fees: $500
- Down payment: $5,000
- Trade-in value: $8,000
- Amount financed: $25,300
- 5-year loan at 4.5%: $471.78 monthly
7.5 Personal Loans
Personal loans are typically unsecured, fixed-rate loans with shorter terms than mortgages. They often have higher interest rates due to the increased risk to lenders.
7.5.1 Personal Loan Considerations
- Origination fees: Often 1-8% of loan amount
- Prepayment penalties: Some loans charge fees for early payoff
- Variable vs. fixed rates: Most personal loans are fixed-rate
📊 Personal Loan with Origination Fee
Loan: $20,000 at 8% for 5 years with 3% origination fee
- Origination fee: $600
- Amount received: $19,400
- Amount owed: $20,000
- Monthly payment: $405.53
- Effective APR: 9.67% (higher due to fee)
7.6 Student Loans
Student loans have unique features including deferment options, income-driven repayment plans, and potential forgiveness programs. Federal student loans use different calculation methods than private loans.
7.6.1 Federal Student Loan Repayment Plans
| Repayment Plan | Payment Calculation | Term |
|---|---|---|
| Standard | Fixed payment (PMT formula) | 10 years |
| Income-Driven | 10-20% of discretionary income | 20-25 years |
| Graduated | Starts low, increases every 2 years | 10 years |
| Extended | Fixed or graduated | 25 years |
7.7 Business Loans
Business loans come in various forms, each with different calculation methods and repayment structures.
7.7.1 SBA Loan Calculations
SBA loans often have variable rates tied to prime rate plus a margin. The calculation includes SBA guarantee fees.
SBA Loan Rate
7.7.2 Equipment Financing
Equipment loans are secured by the equipment being financed and often have rates based on the equipment type and borrower creditworthiness.
💡 Loan Comparison Strategy
When comparing different loan types, always calculate the Annual Percentage Rate (APR) to account for fees and different compounding methods. The APR provides a standardized way to compare the true cost of different loan products.
Understanding the specific calculation methods for different loan types helps you choose the most appropriate financing for your needs. Use our specialized calculators for different loan types: Mortgage Calculator, Personal Loan Calculator, and Debt Payoff Calculator to analyze your specific scenarios.
8. Advanced Calculation Techniques
Mastering advanced loan calculation techniques separates financial professionals from casual borrowers. These sophisticated methods help you analyze complex scenarios, optimize loan structures, and make strategic financial decisions that can save thousands of dollars over time. Advanced calculations also enable you to understand and negotiate complex loan products with confidence.
8.1 Present Value and Future Value Calculations
Present value (PV) and future value (FV) calculations are fundamental to understanding loan economics. These concepts help you compare different payment options and understand the time value of money in loan contexts.
Present Value Formula
Future Value Formula
Where r = periodic interest rate, n = number of periods
📊 Present Value Application
Scenario: Should you pay $10,000 now or $12,000 in 3 years? (Assuming 5% annual return)
- PV of $12,000 in 3 years = $12,000 / (1.05)^3
- PV = $12,000 / 1.1576 = $10,367
- Decision: Pay $10,000 now (saves $367 in present value)
8.2 Net Present Value (NPV) for Loan Decisions
NPV analysis helps evaluate the total economic impact of loan decisions by considering all cash flows over time, discounted to present value.
NPV Formula for Loans
Where t = time period, r = discount rate
📊 NPV Loan Analysis
Comparing two loan options for $100,000:
Option A: 4% for 30 years (Payment: $477.42)
Option B: 4.5% for 15 years (Payment: $764.99)
NPV Analysis (using 3% discount rate):
- Option A NPV: -$134,892
- Option B NPV: -$118,456
- Option B is better by $16,436 in present value terms
8.3 Internal Rate of Return (IRR) Calculations
IRR represents the effective interest rate of a loan when considering all fees, points, and cash flows. It's particularly useful for comparing loans with different fee structures.
IRR Calculation
Solved iteratively using financial calculators or software
8.4 Loan-to-Value (LTV) and Debt-to-Income (DTI) Calculations
These ratios are crucial for loan qualification and risk assessment:
Key Ratio Formulas
📊 Ratio Calculations
Mortgage Application:
- Home value: $400,000
- Loan amount: $320,000
- LTV = ($320,000 / $400,000) × 100 = 80%
- Monthly income: $8,000
- Total debt payments: $2,400
- DTI = ($2,400 / $8,000) × 100 = 30%
8.5 Break-Even Analysis for Refinancing
Break-even analysis determines how long it takes for refinancing savings to offset closing costs:
Refinancing Break-Even Formula
📊 Refinancing Break-Even Analysis
Current loan: $250,000 at 5.5%, payment = $1,419.47
New loan: $250,000 at 4.0%, payment = $1,193.54
- Monthly savings: $1,419.47 - $1,193.54 = $225.93
- Closing costs: $4,500
- Break-even: $4,500 / $225.93 = 19.9 months
- If you plan to stay longer than 20 months, refinancing makes sense
8.6 Prepayment Analysis and Optimization
Advanced prepayment analysis helps determine the optimal strategy for extra payments:
8.6.1 Marginal Interest Rate Analysis
Calculate the effective return on prepayments by comparing interest saved to alternative investments:
Prepayment Return Formula
For tax-deductible loans like mortgages
8.6.2 Optimal Prepayment Timing
Early loan payments save more interest than later payments due to amortization structure:
📊 Prepayment Timing Analysis
$300,000 mortgage at 4.5% for 30 years
$10,000 extra payment impact:
- Year 1: Saves $31,411 in interest, reduces term by 4.2 years
- Year 10: Saves $18,234 in interest, reduces term by 2.8 years
- Year 20: Saves $6,891 in interest, reduces term by 1.1 years
8.7 Monte Carlo Analysis for Variable Rate Loans
Monte Carlo simulation helps analyze the potential range of outcomes for variable-rate loans by modeling thousands of possible interest rate scenarios.
💡 Monte Carlo Application
Use Monte Carlo analysis to understand the potential payment ranges for ARMs. This helps you prepare for worst-case scenarios and make informed decisions about rate caps and loan structures.
8.8 Tax-Adjusted Loan Calculations
For tax-deductible loans, the after-tax cost is lower than the stated interest rate:
After-Tax Interest Rate
📊 Tax-Adjusted Calculation
Mortgage: 4.5% interest rate, 24% marginal tax rate
- After-tax rate = 4.5% × (1 - 0.24) = 4.5% × 0.76 = 3.42%
- This affects investment vs. prepayment decisions
8.9 Sensitivity Analysis
Sensitivity analysis examines how changes in key variables affect loan outcomes:
| Variable Change | Payment Impact | Total Interest Impact |
|---|---|---|
| +0.5% Interest Rate | +$87/month | +$31,320 |
| -5 Year Term | +$524/month | -$89,440 |
| +$50,000 Principal | +$253/month | +$91,080 |
These advanced calculation techniques provide the analytical foundation for sophisticated loan management and optimization strategies. Use our ROI Calculator and Compound Interest Calculator to perform advanced analyses for your specific situations.
9. Real-World Examples and Case Studies
Real-world loan scenarios often involve complex combinations of the principles we've discussed. These comprehensive case studies demonstrate how to apply loan calculation techniques to actual financial decisions, showing the practical impact of different choices and strategies.
9.1 Case Study: First-Time Home Buyer
📊 The Johnson Family Home Purchase
Situation: The Johnsons want to buy a $425,000 home. They have $85,000 for a down payment and excellent credit (750+ score).
Loan Options Analysis:
Option 1: Conventional 30-Year Fixed
- Loan amount: $340,000 (80% LTV)
- Interest rate: 4.25%
- Monthly P&I: $1,672.28
- No PMI required
- Total interest over 30 years: $262,020
Option 2: 15-Year Fixed
- Loan amount: $340,000
- Interest rate: 3.75%
- Monthly P&I: $2,472.84
- Total interest over 15 years: $105,111
- Interest savings vs. 30-year: $156,909
Option 3: 5/1 ARM
- Loan amount: $340,000
- Initial rate: 3.5% (first 5 years)
- Initial monthly P&I: $1,526.57
- Rate caps: 2% periodic, 6% lifetime
- Potential maximum payment: $2,271.16
9.1.1 Decision Analysis
The Johnsons need to consider several factors:
- Cash flow: Can they afford the higher 15-year payment?
- Opportunity cost: Could they earn more than 4.25% investing the payment difference?
- Risk tolerance: Are they comfortable with ARM payment uncertainty?
- Time horizon: How long do they plan to stay in the home?
💡 Johnson Family Recommendation
Given their stable income and long-term plans, the 15-year fixed loan offers the best value despite higher payments. The $156,909 interest savings significantly outweighs the payment difference, and they'll own their home outright 15 years sooner.
9.2 Case Study: Business Equipment Financing
📊 TechStart Company Equipment Purchase
Situation: TechStart needs $150,000 in manufacturing equipment. They're comparing financing options vs. cash purchase.
Option 1: Equipment Loan
- Amount: $150,000
- Rate: 6.5% fixed
- Term: 5 years
- Monthly payment: $2,935.49
- Total payments: $176,129
- Tax benefit: Interest deductible (25% tax rate)
- After-tax cost: $19,597 (interest × 0.75)
Option 2: Equipment Lease
- Monthly lease payment: $3,200
- Term: 5 years
- Total lease payments: $192,000
- Tax benefit: Full deductibility
- After-tax cost: $144,000
- No ownership at end
Option 3: Cash Purchase
- Immediate cost: $150,000
- Depreciation benefit: $30,000 annually (5-year MACRS)
- Tax savings: $37,500 over 5 years
- Net cost: $112,500
- Opportunity cost: Lost investment returns on $150,000
9.2.1 NPV Analysis
Using a 8% discount rate (company's cost of capital):
| Option | NPV of Costs | Ownership | Flexibility |
|---|---|---|---|
| Equipment Loan | $127,845 | Yes | Medium |
| Equipment Lease | $115,200 | No | High |
| Cash Purchase | $119,250 | Yes | Low |
9.3 Case Study: Student Loan Optimization
📊 Sarah's Student Loan Strategy
Situation: Sarah graduated with $85,000 in student loans across multiple servicers with different rates.
Current Loan Portfolio:
- Federal Loan A: $35,000 at 4.5%
- Federal Loan B: $25,000 at 5.5%
- Private Loan: $25,000 at 7.2%
Repayment Strategy Analysis:
Strategy 1: Minimum Payments
- Total monthly payment: $918.33
- Payoff time: 10 years
- Total interest: $25,200
Strategy 2: Debt Avalanche (Highest Rate First)
- Extra $300/month to private loan first
- Private loan paid off: 4.2 years
- Total interest saved: $8,450
- Overall payoff time: 7.8 years
Strategy 3: Refinancing + Avalanche
- Refinance private loan to 5.8%
- Apply avalanche method
- Total interest saved: $12,200
- Payoff time: 7.5 years

9.4 Case Study: Retirement Planning with Mortgage
📊 The Martinez Pre-Retirement Decision
Situation: The Martinez family (ages 55 and 53) have 12 years left on their $180,000 mortgage at 4.8%. They're debating whether to pay it off early or invest extra money for retirement.
Current Mortgage Details:
- Remaining balance: $180,000
- Interest rate: 4.8%
- Monthly payment: $1,567.32
- Remaining term: 12 years
- Total remaining interest: $45,122
Available Options:
Option 1: Extra Mortgage Payments
- Extra payment: $800/month
- New payoff time: 6.8 years
- Interest saved: $22,890
- Guaranteed return: 4.8%
Option 2: Investment Strategy
- Invest $800/month in retirement accounts
- Expected return: 7% annually
- Value after 12 years: $152,847
- Net benefit over mortgage payoff: $129,957
Option 3: Hybrid Approach
- $400/month extra mortgage payment
- $400/month to investments
- Mortgage paid off: 8.9 years
- Investment value: $76,424
- Balanced risk and return
9.5 Case Study: Small Business Loan Comparison
📊 Restaurant Expansion Financing
Situation: Maria's Restaurant needs $200,000 for expansion. She's comparing different business loan options.
Option 1: SBA 7(a) Loan
- Amount: $200,000
- Rate: Prime + 2.75% (currently 6.25%)
- Term: 10 years
- SBA guarantee fee: $5,000
- Monthly payment: $2,267.33
- Total cost: $277,080
Option 2: Bank Term Loan
- Amount: $200,000
- Rate: 8.5% fixed
- Term: 7 years
- Origination fee: $4,000
- Monthly payment: $3,089.75
- Total cost: $262,296
Option 3: Equipment Financing + Line of Credit
- Equipment loan: $120,000 at 7.2% for 7 years
- Line of credit: $80,000 at Prime + 1% (variable)
- Combined monthly payment: ~$2,850
- Flexibility for working capital needs
💡 Case Study Insights
These real-world examples demonstrate that loan decisions involve more than just interest rates. Consider cash flow, tax implications, risk tolerance, and strategic objectives when making financing decisions.
Each case study illustrates different aspects of loan analysis and decision-making. Use our comprehensive suite of calculators to analyze your specific scenarios: Mortgage Calculator, Business Loan Calculator, and Debt Payoff Calculator.
10. Professional Tools and Resources
Having access to the right tools and resources is essential for accurate loan calculations and informed financial decision-making. Professional-grade calculators, spreadsheet templates, and analytical tools can save time, reduce errors, and provide insights that manual calculations might miss. This section covers the most valuable tools available for loan analysis and management.
10.1 Essential Online Calculators
Professional online calculators provide instant, accurate results for complex loan scenarios. Our comprehensive calculator suite at Proculator.com offers specialized tools for every type of loan calculation:
🧮 Professional Calculator Suite
Access our complete collection of professional-grade financial calculators:
Comprehensive Loan Calculator Advanced Mortgage Calculator Compound Interest Calculator Debt Payoff Optimizer Interest Rate Calculator10.1.1 Loan Calculator Features
Our Professional Loan Calculator includes:
- Multiple payment frequencies: Monthly, bi-weekly, weekly calculations
- Extra payment analysis: See the impact of additional principal payments
- Amortization schedules: Detailed payment breakdowns over the loan term
- Comparison tools: Side-by-side analysis of different loan scenarios
- Tax considerations: After-tax cost calculations for deductible loans
10.1.2 Specialized Mortgage Tools
Our Advanced Mortgage Calculator provides:
- PITI calculations: Principal, interest, taxes, and insurance
- PMI analysis: Private mortgage insurance calculations and removal timing
- ARM modeling: Adjustable-rate mortgage payment projections
- Refinancing analysis: Break-even calculations and savings projections
- Affordability assessment: Maximum loan amount based on income and debt ratios
10.2 Spreadsheet Templates and Models
Spreadsheet templates provide flexibility for custom loan analysis and scenario modeling. Key templates include:
10.2.1 Amortization Schedule Template
A comprehensive Excel template should include:
- Input cells for loan amount, rate, and term
- Automatic payment calculation using PMT function
- Monthly breakdown of principal and interest
- Running balance calculations
- Summary statistics (total interest, payoff date)
- Extra payment scenarios
10.2.2 Loan Comparison Spreadsheet
Essential features for comparing multiple loan offers:
- Side-by-side loan parameter inputs
- APR calculations including fees
- Total cost comparisons
- Cash flow analysis
- Break-even calculations
- Sensitivity analysis tables
10.3 Financial Calculator Functions
Understanding financial calculator functions enables quick, accurate calculations:
| Function | Purpose | Key Variables |
|---|---|---|
| PMT | Calculate payment amount | Rate, periods, present value |
| PV | Calculate present value | Rate, periods, payment, future value |
| FV | Calculate future value | Rate, periods, payment, present value |
| RATE | Calculate interest rate | Periods, payment, present value, future value |
| NPER | Calculate number of periods | Rate, payment, present value, future value |
10.4 Mobile Apps and Software
Mobile applications provide convenient access to loan calculations on-the-go:
10.4.1 Professional Features to Look For
- Offline functionality: Calculate without internet connection
- Save and compare: Store multiple loan scenarios
- Export capabilities: Share results via email or PDF
- Amortization schedules: Detailed payment breakdowns
- Extra payment modeling: Prepayment impact analysis
10.5 Specialized Business Tools
For business loan analysis, consider these specialized tools:
10.5.1 Cash Flow Analysis Tools
Business loan decisions require cash flow modeling:
- Seasonal adjustment: Account for business cycles
- Growth projections: Model expanding revenue
- Debt service coverage: Ensure adequate cash flow
- Scenario analysis: Best/worst case modeling
Use our ROI Calculator to analyze the return on investment for business loans and equipment financing.
10.6 Tax Calculation Resources
Tax implications significantly affect loan economics:
10.6.1 Deduction Calculators
For tax-deductible loans, calculate after-tax costs:
- Mortgage interest deduction: Home loan interest benefits
- Business loan interest: Commercial loan deductibility
- Investment loan interest: Margin loan deductions
- Student loan interest: Education loan benefits
Our Tax Calculator helps determine the after-tax impact of loan interest deductions.
10.7 Data Sources and Market Information
Stay informed about current market conditions:
10.7.1 Interest Rate Resources
- Federal Reserve data: Prime rate and federal funds rate
- Treasury rates: Benchmark rates for various terms
- Mortgage rate surveys: Current home loan rates
- Bank rate comparisons: Competitive rate shopping
10.7.2 Economic Indicators
Understanding economic trends helps with loan timing:
- Inflation data: Real vs. nominal interest rates
- Employment statistics: Economic stability indicators
- Housing market data: Property value trends
- Credit market conditions: Lending availability
💡 Tool Selection Strategy
Choose tools based on your specific needs: simple calculators for quick estimates, spreadsheets for detailed analysis, and professional software for complex scenarios. Always verify results with multiple tools for important financial decisions.
10.8 Integration and Workflow
Develop an efficient workflow using multiple tools:
- Initial screening: Use online calculators for quick comparisons
- Detailed analysis: Build spreadsheet models for complex scenarios
- Verification: Cross-check results with alternative tools
- Documentation: Save and organize analysis for future reference
- Monitoring: Track actual performance against projections
Our comprehensive calculator suite at Proculator.com provides all the tools you need for professional loan analysis. Start with our Main Loan Calculator and explore specialized tools like our Compound Interest Calculator and Debt Optimization Tool for complete financial analysis.
11. Optimization Strategies and Best Practices
Mastering loan calculations is only the beginning. The real value comes from applying this knowledge to optimize your borrowing strategy, minimize costs, and maximize financial benefits. This section covers advanced strategies that can save thousands of dollars over the life of your loans and help you make smarter financial decisions.
11.1 Interest Rate Optimization
Even small differences in interest rates can have massive impacts on total loan costs. Understanding how to secure the best rates and when to act on rate opportunities is crucial for loan optimization.
11.1.1 Credit Score Impact Analysis
Your credit score directly affects the interest rates you'll qualify for. Understanding this relationship helps you prioritize credit improvement efforts:
| Credit Score Range | Typical Rate Premium | $300K Mortgage Cost Impact |
|---|---|---|
| 760-850 (Excellent) | Best available rates | Baseline |
| 700-759 (Good) | +0.25% to +0.50% | +$15,000 to +$30,000 |
| 650-699 (Fair) | +0.75% to +1.25% | +$45,000 to +$75,000 |
| 600-649 (Poor) | +1.50% to +2.50% | +$90,000 to +$150,000 |

11.1.2 Rate Shopping Strategy
Effective rate shopping requires a systematic approach:
- Timing concentration: Complete all rate inquiries within a 14-45 day window to minimize credit score impact
- Compare APRs, not just rates: APR includes fees and provides a more accurate cost comparison
- Negotiate fees: Many lender fees are negotiable, especially for well-qualified borrowers
- Consider points: Calculate break-even period for paying points to reduce rates
- Lock timing: Understand rate lock periods and extension options
11.2 Loan Term Optimization
Choosing the optimal loan term involves balancing monthly payment affordability with total interest costs:
📊 Term Optimization Analysis
$250,000 loan at 4.5% interest:
| Term | Monthly Payment | Total Interest | Monthly Savings vs 30yr |
|---|---|---|---|
| 15 years | $1,912.48 | $94,246 | -$645.81 |
| 20 years | $1,581.59 | $129,582 | -$314.92 |
| 30 years | $1,266.71 | $206,016 | Baseline |
Key insight: The 15-year loan saves $111,770 in interest but requires $645.81 more monthly
11.2.1 Hybrid Term Strategy
Consider taking a longer-term loan but making payments as if it were shorter-term. This provides flexibility while achieving interest savings:
💡 Flexible Term Strategy
Take a 30-year mortgage but pay the 15-year amount when possible. This gives you the flexibility to reduce payments during financial stress while achieving most of the interest savings when cash flow allows.
11.3 Prepayment Strategies
Strategic prepayments can dramatically reduce total interest costs and loan terms:
11.3.1 Optimal Prepayment Methods
- Extra principal payments: Apply additional amounts directly to principal
- Bi-weekly payments: Make 26 payments annually instead of 12
- Annual lump sums: Use bonuses, tax refunds, or windfalls
- Round-up payments: Round monthly payments to nearest $50 or $100
📊 Bi-Weekly Payment Impact
$300,000 mortgage at 4.5% for 30 years:
- Monthly payments: $1,520.06 × 12 = $18,240.72 annually
- Bi-weekly payments: $760.03 × 26 = $19,760.78 annually
- Extra annual payment: $1,520.06
- Payoff time reduction: 4.5 years earlier
- Interest savings: $123,312
11.3.2 Prepayment vs. Investment Analysis
Determine whether to prepay loans or invest extra money:
Prepayment Decision Formula
📊 Prepayment vs. Investment Example
Scenario: $1,000 extra monthly, 4.5% mortgage rate, 25% tax bracket
- After-tax mortgage rate: 4.5% × (1 - 0.25) = 3.375%
- Investment threshold: Need >3.375% expected return to invest instead
- Conservative portfolio (5% expected): Invest the extra money
- Risk consideration: Mortgage prepayment is guaranteed return
11.4 Refinancing Optimization
Strategic refinancing can reduce rates, change terms, or access equity:
11.4.1 Refinancing Decision Matrix
| Rate Reduction | Break-Even Period | Recommended Action |
|---|---|---|
| 0.25% - 0.50% | 3-5 years | Consider if staying long-term |
| 0.50% - 0.75% | 2-3 years | Likely beneficial |
| 0.75% - 1.00% | 1-2 years | Strong candidate |
| 1.00%+ | <1 year | Refinance immediately |
11.4.2 Cash-Out Refinancing Strategy
Use home equity strategically:
- Debt consolidation: Pay off higher-rate debt
- Home improvements: Increase property value
- Investment opportunities: Real estate or business ventures
- Education funding: Lower-cost education financing
Use our Mortgage Refinancing Calculator to analyze refinancing scenarios and break-even periods.
11.5 Debt Consolidation Strategies
Strategic debt consolidation can reduce overall interest costs and simplify payments:
11.5.1 Consolidation Methods
- Personal loans: Fixed-rate consolidation for credit cards
- Home equity loans: Lower rates using home as collateral
- Balance transfers: Promotional rates on credit cards
- Cash-out refinancing: Include debt in mortgage refinancing
📊 Debt Consolidation Analysis
Current Debt Portfolio:
- Credit Card A: $15,000 at 18.9%
- Credit Card B: $8,000 at 22.4%
- Personal Loan: $12,000 at 12.5%
- Total debt: $35,000
- Weighted average rate: 17.2%
- Current monthly payments: $1,247
Consolidation Option: $35,000 personal loan at 8.5% for 5 years
- New monthly payment: $719
- Monthly savings: $528
- Interest savings: $27,840 over 5 years
Our Debt Payoff Calculator helps analyze different consolidation strategies and payoff methods.
11.6 Tax Optimization Strategies
Maximize tax benefits from loan interest deductions:
11.6.1 Mortgage Interest Deduction Optimization
- Timing strategies: Bunch payments in high-income years
- Home equity debt: Deductible if used for home improvements
- Points deduction: Immediate vs. amortized deduction strategies
- Refinancing considerations: Impact on deduction timing
11.6.2 Business Loan Tax Strategies
- Section 179 deduction: Immediate expensing of equipment
- Interest deduction timing: Match with business income
- Loan vs. lease analysis: Tax implications of each option
11.7 Risk Management in Loan Strategy
Balance optimization with risk management:
11.7.1 Interest Rate Risk
- Fixed vs. variable rate decisions: Based on rate environment and risk tolerance
- Rate caps and floors: Understanding ARM protection features
- Hedging strategies: Using financial instruments to manage rate risk
11.7.2 Liquidity Risk
- Emergency fund maintenance: Don't over-prepay at expense of liquidity
- Credit line access: Maintain available credit for emergencies
- Payment flexibility: Choose loans with prepayment options
💡 Optimization Balance
The best loan strategy balances cost minimization with risk management and financial flexibility. Don't optimize purely for lowest cost if it creates unacceptable risk or reduces financial flexibility.
11.8 Monitoring and Adjustment Strategies
Loan optimization is an ongoing process:
- Regular rate monitoring: Track market rates for refinancing opportunities
- Payment strategy review: Adjust prepayment strategy based on financial changes
- Tax situation updates: Modify strategy based on tax law changes
- Life event adjustments: Adapt strategy for major life changes
- Performance tracking: Monitor actual vs. projected loan performance
Implementing these optimization strategies can save tens of thousands of dollars over the life of your loans. Use our comprehensive calculator suite to model different strategies: Loan Calculator, Interest Calculator, and Tax Calculator for complete optimization analysis.
12. Conclusion: Mastering Your Financial Future
Congratulations! You've now completed a comprehensive journey through the world of loan calculations and financial optimization. The knowledge and skills you've gained from this guide represent a significant investment in your financial future—one that will pay dividends for years to come through better borrowing decisions, optimized loan strategies, and substantial cost savings.